compound interest calculator for retirement planning
Readers like you help support Lifespectrum360.com. When you purchase using links on our site, we may earn an affiliate commission. Read More.
Compound Interest Calculator
Number of Years of Investment:
Maturity Amount:
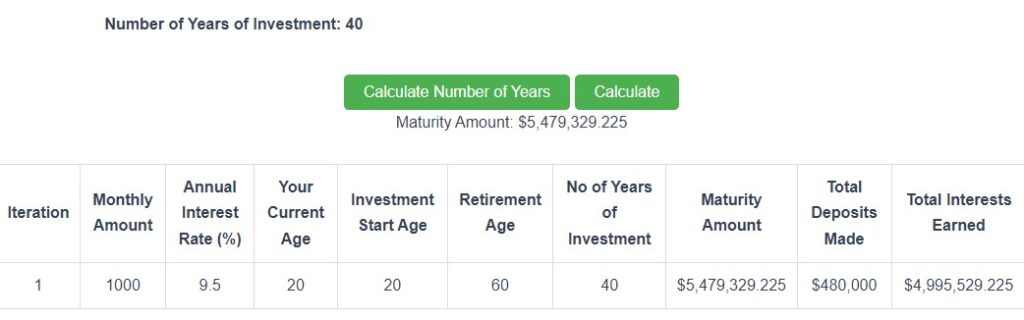
| Iteration | Monthly Amount | Annual Interest Rate (%) | Your Current Age | Investment Start Age | Retirement Age | No of Years of Investment | Maturity Amount | Total Deposits Made | Total Interests Earned |
|---|
| Iteration | Month | Monthly Deposit | Interest Earned | Total Amount |
|---|
How to use compound interest calculator?
Input values
- Monthly Amounts in dollars – ‘1000’ will appear by default. You can change the number to your preferred amount of monthly savings.
- Annual Interest Rate – Enter the annual interest rate (in percentage) you expect from your investments. 9.5% is shown by default because the S&P 500 has given returns at an annualized rate of around 9.5% over the last 30 years.
- Enter your Current Age, Investment Start Age, and expected Retirement Age in years.

Calculate Buttons
There Are Two Calculate Buttons Available In The Compound Interest Calculator – Calculate No Of Years, Calculate.
- Click on Calculate Number Of Years to get the number of years for which you will be investing. It is the difference between your investment start age and planned retirement age. If the number of years of investment is insufficient, either reduce your investment start age or increase your retirement age.
- Click on Calculate to get the Maturity Amount. The maturity amount will appear below the button. A table will capture all the details of the calculation.
Once you get the maturity amount, If you want to see how your investment grew each month, click on the Display Monthly Breakup button below the results table in our compound interest calculator.
Make the right decision
The most important thing for you is to decide on the right combination of investment amount, investment period, and rate of return. Compound Interest Calculator will help you enter different combinations and see the results yourself before you make a decision.
E.g.
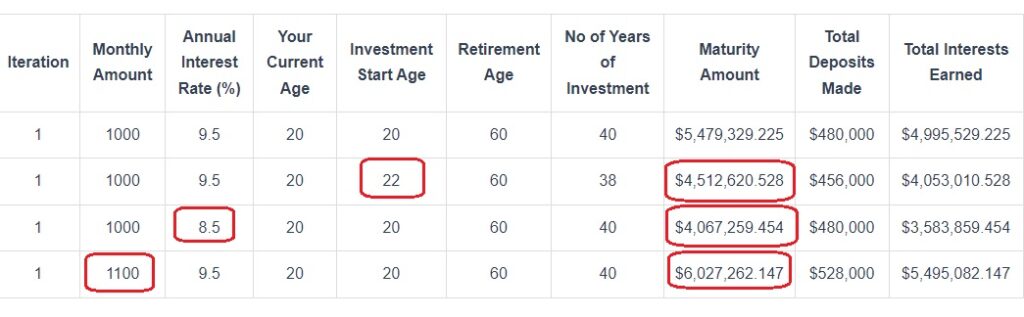
Scenario 1: You can see that $1,000 a month will fetch around $5.5 million in 20 years at a 9.5% annual interest rate.
Scenario 2: However, If you reduce your investment period by just two years by delaying your investment start age from 20 to 22 years, your maturity amount gets reduced by over $900 K (from $5.5 million to $ 4.5 million). If you start investing two years earlier, you will gift yourself close to a million dollars at retirement age. TIME FOR THE INVESTMENT IS BETTER THAN TIMING THE INVESTMENT.
Scenario 3: If your investment earns 1% less, you are losing close to $1.5 million (from $5.5 million to $4 million). Choose an investment that gives a better return over the long term. ( Visit our Next Gen Personal Finance suite of solutions to choose the best investment for you.)
Scenario 4: If you increase your monthly savings by just $100, you will get an additional $500 K over 20 years. Save as much as possible and give yourself a fat check as a gift at retirement time. Check our Budgeting Calculator to plan your monthly income and expenses and maximize your savings.
FAQ
Compound Interest is also called “Interest On Interest”. The interest for the first period (year) is added to the principal at the end of the year and starts earning interest for the new amount in the next year.
e.g. If you have invested $ 100 in a Bank Fixed Deposit at 5% interest, then at the end of the first year, the interest will be $5.00.
The principal for the next period will be = Original Principal + First year interest = 100 + 5 = $105.00
In the 2nd year, the 5% interest will be applied to the new principal $105. So interest for the 2nd year will be = 105 * 0.05 = $ 5.25.
Note that the interest in the second year is higher than the interest in the first year. This is called the power of compounding. As the investment period grows, the effect will be more. There will be a time when the interest component will be more than your contributions. To see the effect, click on Display Monthly Breakup. The compounding effect meaning is popular and applied in our compound interest calculator.
The Rule of 72 is a quick method to estimate how long it will take for a particular amount of money to double with an annual interest rate. Any investment with a fixed rate and compound interest within a reasonable range is eligible for use. To find the number of years it will take to double, divide 72 by the annual rate of return.
E.g. it will take about nine (72 / 8) years for $100 with a fixed rate of return of 8% to grow to $200. Remember that an “8” represents 8%, so users should not convert it to decimal. Therefore, one would use “8” rather than “0.08”.
Rule of 72 also works on the same method of compounding that our compound interest calculator uses. Additionally, be mindful that the Rule of 72 is an approximation, not exact.
If a person deposits $1000.00 at the beginning of the year @5% annual interest rate, then at the end of 2 years,
P = 1000 r = 0.05 (= 5% or 5/100) n = 2 years
Then, by applying the above formula, the maturity amount will be –
(1+0.05)^2 = $1102.5
In a single browser session, one can compare the five results to determine the savings amount, number of years, and expected annual return on investments for a desired sum at retirement.
The three ways to harness the power of compounding for a better future are –
- Start your investment early – You can see from the sample results from the compound interest calculator that, by reducing the investment period by just two years, the person is losing close to a million USD in maturity value. Always allow as much time as possible for your investment to grow.
- Invest as much as possible – The more you invest, the more you will get. As you can see, by increasing the monthly savings amount by just $100, the retirement kitty becomes fatter by nearly $500 K.
- Earn return as much as possible – Your investments should return as much as possible. In the same example, you can see, a reduction in interest rate by 1%, removes close to $ 1.5 million from the retirement kitty.
For more details, refer to our Blog here.
